CVPR2022 TokenCut

Self-supervised Transformers for Unsupervised Object Discovery Using Normalized Cut

使用归一化割的无监督对象发现自监督Transformers

Abstract

tokens作为nodes，edge是token间的similarity

使用归一化图割(normalized graph-cut)对前景对象进行分割,对自相似的区域进行分组，使用具有广义特征分解的谱聚类来解决graph-cut问题，并表明第二小特征值对应的特征向量提供了切割结果，因为它的绝对值表示token属于前景对象的可能性。

作者提到了两个和Transformer相关的以往的工作

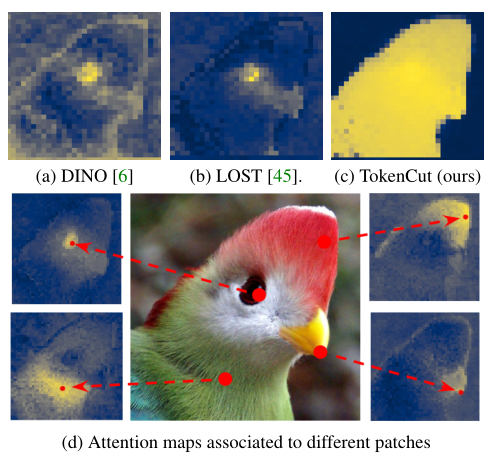
DINO(a)，使用自蒸馏损失进行训练时，最后一层的class token相关联的attention map表明了显著的前景区域
- 但这种attention map是嘈杂的，且不清楚是否可以用于无监督的对象发现
LOST(b)，使用patches的相关关系建立图，使用节点的反度来分割目标，启发式种子扩展策略用于克服噪声并检测前景对象的单个边界框
- 依赖特定节点的注意力图

表示不同节点关联的attention map包含了有意义的信息(d)，本文通过使用特征分解将图投影到低维子空间中来使用整个图中的信息，这种投影可以与归一化切割(Ncut) 一起使用，以显着改善前景/背景分割(c)

主要贡献：

以patch为节点，每个patch使用DINO的特征描述，每个patch和其相邻的patch相连，边使用余弦相似度计算得到

$\mathcal{E}_{i, j}=\left\{\begin{array}{ll}
1, & \text { if } S\left(v_{i}, v_{j}\right) \geq \tau \\
\epsilon, & \text { else }
\end{array}\right.$

$S\left(v_{i}, v_{j}\right)=\frac{v_{i} v_{j}}{\left|v_{i}\right|_{2}\left|v_{j}\right|_{2}}$

$S(v_i,v_j)$代表两个节点的余弦相似度，$ \tau$是一个超参数，$ \epsilon=1e-5$代表一个非常小的值，保证图是全连接的。

作者认为，空间信息已通过 Transformer中的位置编码隐式包含在特征中

在构造的图上应用Ncut算法，获取广义特征系统的第二小的特征向量，可以看作是潜在对象的注意力图

作者假设图像中至少有一个对象，且该对象占据了前景区域。

从图像中分割出前景对象需要解决三个问题：

需要确定把图划分为两个子图的方法
- 使用投影到第二小的特征向量上的简单平均值来确定切割图的相似度值
  - 平均值$\bar{y_1}=\frac{1}{N}\sum_iy_1^i$
  - 分割$A=\left\{v_{i} \mid \mathbf{y}_{1}^{i} \leq \overline{\mathbf{y}_{1}}\right\} \text { and } B=\left\{v_{i} \mid \mathbf{y}_{1}^{i}>\overline{\mathbf{y}_{1}}\right\}$
给定图的两个子图，需要确定哪一个子图代表前景
- 前景包含着显著对象，并假设其与整个图有更少的联系
  - 直观来说，有更小的度的token更可能是前景
  - 因此前景对象的特征向量的绝对值应该大于背景对象的特征向量，使用最大绝对值$v_{max}$来选择前景和最显著对象。
如果前景检测到多个连通分量，必须识别出最显著的对象

总结起来的4步

Normalized Cuts将图像分割问题视作图割问题，将像素视为节点，构建完全连接的无向图，边权代表两个节点间的相似性，NCut最小化将图划分为两个子图的成本，最小化这一成本可以通过求解广义特征值系统完成：

$(D-W) x=\lambda D x$

$\lambda$代表第二小特征值，$x$代表特征向量，$D$代表度矩阵，是一个$N\times N$的对角矩阵,其中元素$d(i)=\sum_{j} W_{i j}$，$W$是$N\times N$的对称矩阵

$G=(V,E)$, V代表顶点vertex，E是边edge, 把G划分为A和B两个子图

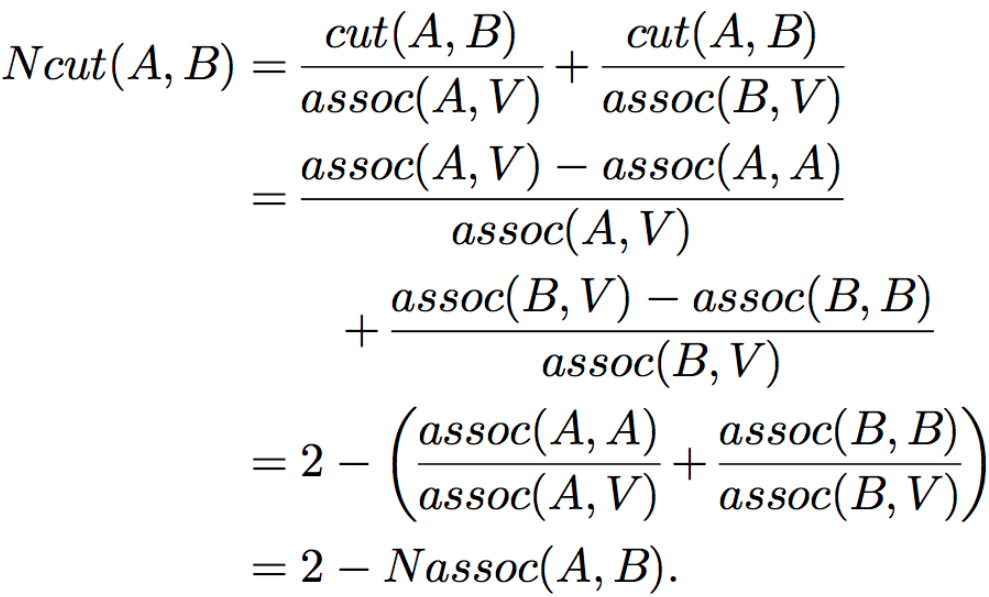
其中$assoc(A,V)=\sum_{u\in A,t\in V}w(u,t)$的含义是A中所有点到图中所有点的边的权重之和，也就是Ncut追求不同子集间点与点的边权重最小值，同时也追求同一子集内部点与点的边权重最大值，避免分割出孤立点、边缘点

TokenCut的一个局限性是它只为一个图像计算一个二进制掩码，因此每个图像只能找到一个对象。