Transformer
核心组件 self-attention
注意力机制实现的两个步骤
计算注意力分布α
- 使用query对输入向量X进行得分计算,通常是内积,评价x与任务的相关程度
- 然后使用softmax计算得到注意力分布α
利用注意力分布对输入向量($X=(x_1,x_2,···,x_n)$)进行加权求和求平均

self-attention则是注意力机制中的一种,其特点是查询向量q是内部的,比如下图是NLP中的一个例子,单词the作为查询向量q,the是输入的句子中的一个词
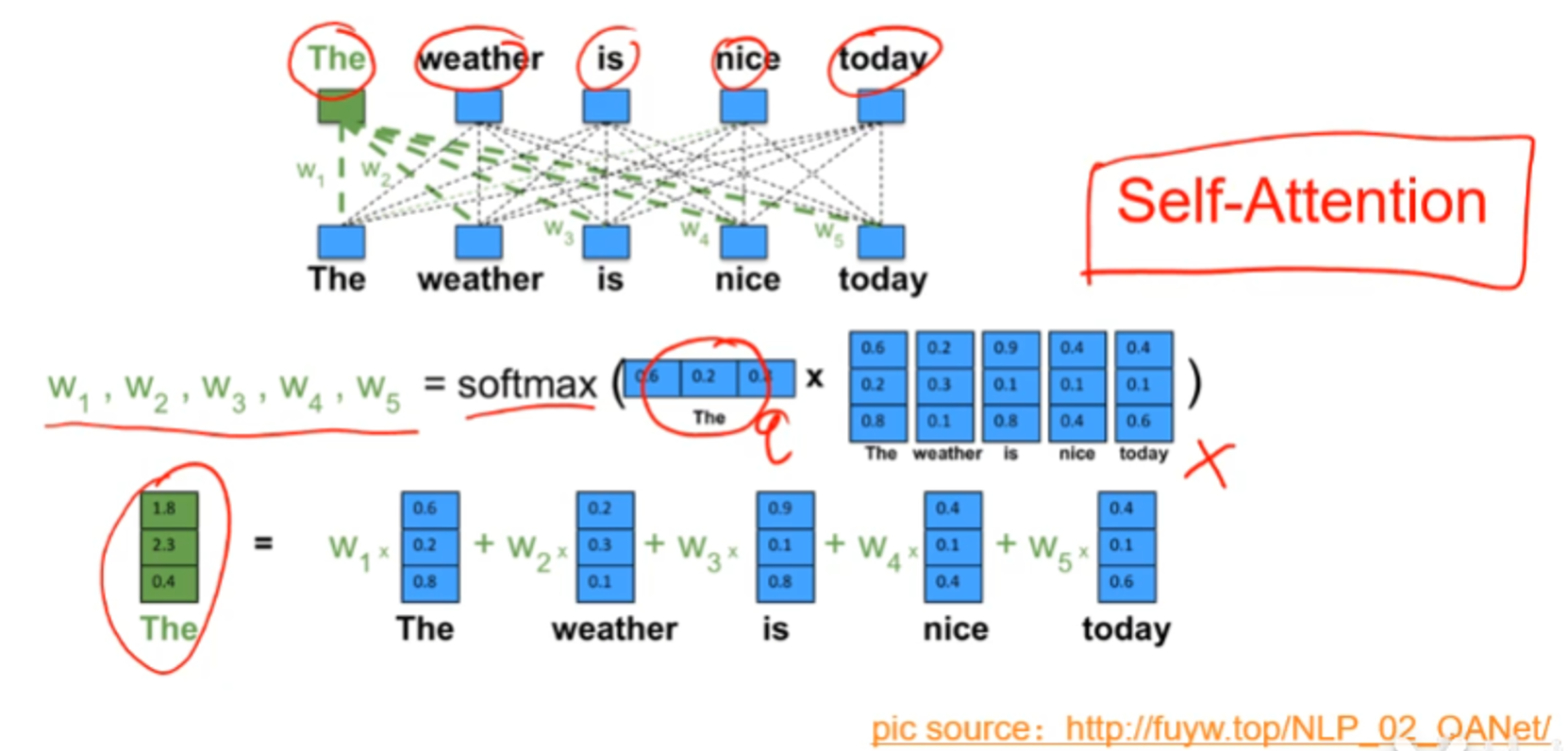
上述的self-attention例子是不带可学习参数的,模型容量小,常用的是其变体——QKV模型
QKV模型
QKV的含义
Query-Key-Value
设输入为$X=(x_1,x_2,···,x_N)$,每个分量x~i~都是D~x~维的向量,下图中的W~q~、W~k~、W~v~是三个可学习的参数矩阵,其作用是将输入分别映射到另一个空间,在这个空间计算依赖关系,经过映射后得到QKV三个矩阵,分别是查询向量矩阵,关键字矩阵和值矩阵。
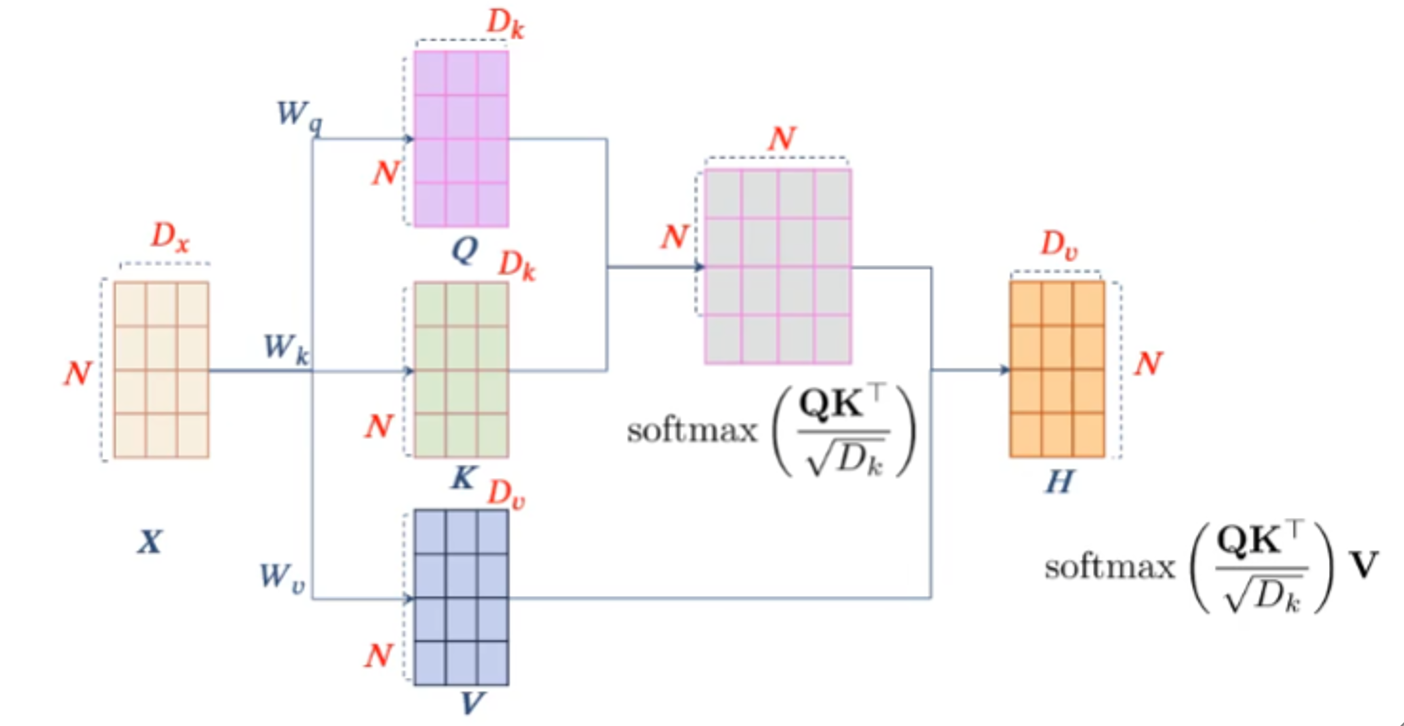
具体计算步骤如下:
输入$X$经过三个参数矩阵映射到了三个空间,其在三个空间中的矩阵表示分别是Q、K、V
计算$softmax(\frac{QK^T}{\sqrt{D_k}})$,其作用是计算N个分量之间的相似度,得到的NxN的矩阵表示了各分量之间的相关程度,也就是注意力分布。
Q和K是输入在不同空间的不同表现形式,做内积得到的是一个非对称的矩阵(有向图模型),比如Q的第一行表示的向量和K的第二行做内积,与K的第一行和Q的第二行内积的结果是不相等的,也就是attention map上对称的两个位置值不相等
$QK^T$表示QK两个矩阵求内积(数量积、点积,对于向量是对应元素相乘再相加,矩阵则是QK^T^这样的形式,两个向量垂直时内积为0,夹角越小越相似,内积越大),除以$\sqrt{D_k}$是为了使梯度更稳定,因为向量维度越大,内积中累加操作得到的值就越大,这并不是我们所希望的,所以除以维度,对内积结果进行约束,然后最后使用softmax得到归一化的注意力分布。

为何除以根号n而不是除以n:
X~N(0,1) aX~N(0,a^2)
假设两个输入向量q和k的每一维都具有零均值和单位方差、并且假设每一维都互相独立,那么这个除sqrt(dk)的操作可以使得运算结果仍然保持零均值和单位方差,因而有利于模型训练的稳定性。

将上一步中得到的注意力分布$softmax(\frac{QK^T}{\sqrt{D_k}})$作为权值加权到输入X经过映射得到的V矩阵,得到输入的上下文表示
multi-headed机制
类似CNN中使用多个卷积核提取特征
- 通过不同的head得到不同的特征表达
- 将得到的特征拼接并使用全连接来降维
transformer整体架构
Transformer核心是self-attention,但相比于self-attention加入了
- 位置信息,具体处理方式为将绝对位置用向量表示,与词嵌入直接相加
- 层规范化,使得神经网络训练更加稳定
- 残差连接
- 逐位的FFN(前馈神经网络),在得到每个词的上下文表示后,需要使用一个两层的MLP(多层感知机)进行特征变换,在所有位置上是共享的,可以看做一个窗口唯一的卷积